Al poseer un sistema formal basado en axiomas, la intención era que pudiera automatizarse la deducción de cualquier verdad matemática, que una máquina dedujera las cosas sin necesidad de que un ser humano, propenso al error, interviniera. La verdad debía poder deducirse por pura manipulación simbólica llevada a cabo con las reglas de la lógica.
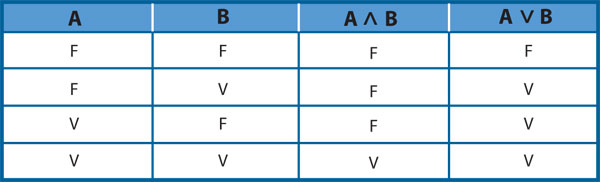
Uno de los lógicos matemáticos que contribuyeron relevantemente en ese sentido fue George Boole —él se dio a la tarea de formular las reglas de manipulación que permitían deducir la verdad o falsedad de expresiones construidas con símbolos que representan enunciados, sin importar lo que los símbolos representaran, se pudieran manipular algebraicamente las expresiones construidas con ellos para deducir nuevas expresiones válidas—. El resultado más útil para la computación fue lo que se conoce como el álgebra de las funciones de conmutación, un caso simple de álgebra de Boole que es, de hecho, un sistema formal. En el álgebra de las funciones de conmutación se poseen al menos dos elementos (típicamente, verdadero y falso, o 1 y 0) y tres operaciones elementales: una operación unaria (que posee un solo operando) llamada negación: si A denota una variable, entonces à denota la negación de A, si A es verdadero o 1, entonces à es falso o 0, respectivamente. Las otras dos operaciones se llaman disyunción y conjunción, y son las que ya se conocen de la lógica simbólica. En la tabla que sigue se muestran las tablas de verdad de estas operaciones en la lógica proposicional.
Cualquier otra función de conmutación puede formularse con base en las tres funciones elementales mencionadas, es decir, la tabla de verdad de cualquier función cuyas variables sean booleanas (falso o verdadero) puede obtenerse combinando estas tres operaciones.
Esto resulta sumamente útil, como se verá en el capítulo dedicado a sistemas de cómputo, pero no es todo lo que se necesita.