Lo que se conoce como computadora es: la caja que contiene el procesador junto al monitor, el teclado y el ratón. A final de cuentas, no es más que una caja negra. ¿Tiene ésta el mismo poder de cómputo que un autómata finito? Ya se discutió anteriormente que un autómata finito sólo puede computar expresiones regulares; cosas tan sencillas como un palíndromo están más allá de su alcance. Asimismo, se argumentó que cualquier caja negra no es más que un autómata finito. ¿Cuál es la solución a esta paradoja? El cerebro mismo, ¿no es una caja negra con la que interactuamos mediante entradas y salidas y, a final de cuentas, de tamaño finito? Una computadora no es más que la realización concreta de una abstracción.
En 1936 el matemático inglés Alan Turing formuló el concepto de la máquina que lleva su nombre. La máquina de Turing es una abstracción fundamental en computación. Con ella se logró capturar lo verdaderamente esencial del concepto de algoritmo. Antes de Turing el concepto era vago, propenso a la ambigüedad; algunos, como el matemático David Hilbert, lo describían como "un procedimiento efectivo". Kurt Gödel se aproximó mejor, describiéndolo como una secuencia finita de deducciones en el terreno de la lógica. Pero la abstracción de Turing logra, por una parte, captar lo mínimo indispensable sin ambigüedades de interpretación y, por otra, formular el concepto de una forma general y simple. Existen otros modelos de lo que significa algoritmo, sorprendentemente varios de los más fundamentales fueron establecidos de manera simultánea, en 1936, pero todos equivalentes al de Turing que es un tipo de máquina de estados.
Por supuesto, la máquina de estados propuesta por Turing debe modelar lo que hoy se conoce como una computadora, y por lo tanto poder computar más cosas que expresiones regulares, así que no puede tener un número finito de estados. Pero ya se dijo varias veces que cualquier caja negra sólo puede tener un número finito de estados. Las computadoras modernas se distinguen por dos cosas:
• Tienen un número de estados inimaginablemente grande: muchísimos millones de millones.
• Se les pueden agregar estados, añadiéndoles memoria.
Alan Turing, en uno de los artículos más importantes del siglo XX, pudo intuir un modelo de la esencia de una computadora antes que ninguna se hubiera construido, a partir de un ejercicio mental, en lo que se considera una de las exposiciones más brillantes de un argumento informal e intuitivo que lleva a una noción precisa y formal. Turing pide imaginar a una persona haciendo matemáticas, sentada en un escritorio. Tiene lápiz y papel donde escribir símbolos. Un matemático va escribiendo símbolos, uno tras otro, quizá borrando o cambiando alguno de vez en cuando. Cuando se le acaba la hoja, toma otra. En principio, cuántas hojas toma, cuántos símbolos escribe, qué tan largo es el cálculo que está haciendo, no están limitados más que por su propio tiempo de vida. Quizá ni eso, ya que otros matemáticos pueden continuar con su trabajo. Eso sí, trabaja con un número de símbolos finito. Cualquier descubrimiento de matemáticas posible se podrá hacer de esta forma, cualquier cómputo, cualquier procesamiento de información. Es así como Turing deriva su modelo de máquina de estados, muy similar a un autómata finito, con la única diferencia de que debe tener "hojas de papel" disponibles, ilimitadamente.
Con más detalle, una máquina de Turing puede visualizarse como una caja negra, que es un autómata finito, llamada unidad de control, que supuestamente representa la mente del matemático. Ésta posee una cabeza de lectura y escritura que recorre una cinta sin fin, representando las hojas de papel. La cinta se puede pensar dividida en celdas de tamaño fijo, en cada una está escrito un símbolo de un conjunto finito, llamado alfabeto. La cabeza recorre la cinta en cualquiera de sus dos direcciones y puede leer de cada celda o escribir en ella un símbolo (del alfabeto de salida). La máquina de Turing inicia con la cabeza colocada en un sitio particular de la cinta llamado celda inicial y la unidad de control en un estado inicial particular; la unidad de control, de acuerdo con las transiciones de su autómata finito, indica, en función del símbolo de entrada sobre el que está la cabeza, cuál debe ser el estado siguiente de la máquina, cuál debe ser el símbolo que debe escribirse en la celda actual y la dirección en la que debe moverse la cabeza. En algún momento, si los datos de entrada fueron "correctos", es decir, concuerdan con lo que la máquina esperaba encontrar en la cinta a partir de la celda inicial, ésta termina llegando a un estado final, y en la cinta se encuentra el resultado de la ejecución del algoritmo. Si los datos de entrada en la cinta no coinciden con lo esperado por la máquina, entonces ésta puede llegar a un estado de error; se puede pensar que llega a un estado en el que se detiene y en un panel lateral despliega el mensaje "la entrada no es aceptada". Una tercera posibilidad es que la máquina no termine, que la entrada haga que la máquina entre en un ciclo infinito en el cual se repiten indefinidamente algunos de los estados, sin llegar nunca al estado final. La idea es que una máquina de Turing es un modelo de una computadora, tal y como las usadas hoy en día. Este modelo logra captar todos los elementos mencionados en el módulo dedicado a los algoritmos, a saber:
• Se poseen datos de entrada. El contenido original de la cinta.
• Se cuenta con un conjunto de estados por los que transita la máquina abstracta durante la ejecución del algoritmo. Un estado está determinado por el contenido de la cinta y el estado del control finito.
• Se producen datos de salida. El contenido de la cinta luego de la ejecución del algoritmo.
• Existe un conjunto finito de instrucciones que le especifican a la máquina, en todo momento, cuáles deben ser las acciones a realizar dado el estado actual y el dato de entrada que recibe, codificadas en el control finito de la máquina.
• El problema que resuelve la máquina es representado por una función f, tal que si la entrada a la máquina es x, cuando la máquina se detiene, en la cinta se encuentra f(x).
En el caso de la máquina de Turing, las instrucciones del último punto sólo dicen "si estando en el estado a, en la celda de la cinta ves el símbolo x, pasar al estado e, escribe el símbolo y, y mueve la cabeza en dirección d". Se tiene un conjunto finito muy bien especificado: a y e están en el conjunto de estados, al que llamaremos Q y que contiene al estado inicial q0 y al estado final qF x y y en el conjunto de símbolos posibles o alfabeto, al que se denominará A; d es una de dos opciones, los elementos del conjunto D = {Izq, Der, Alto}; así que cualquier ambigüedad queda eliminada. Se podría decir que el lenguaje en el que se especifican los algoritmos a una máquina de Turing está hecho de quintetas de la forma (a, x, e, y, d).
Llama la atención que la cinta de la máquina sea infinita. La intención de esto es que el poder de cómputo no se vea limitado a priori, como se explicó con el ejemplo del matemático y sus hojas de papel. Lo importante es que, por supuesto, en cualquier momento durante la ejecución de una máquina de Turing sólo una sección finita de la cinta se utiliza.
Un ejemplo de máquina de Turing
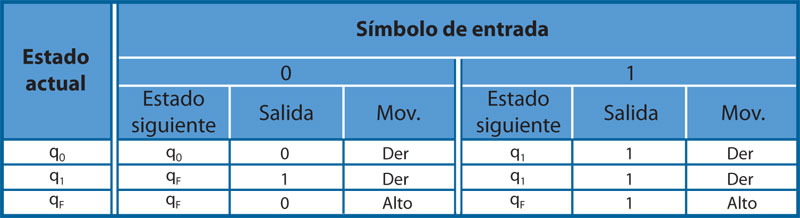
Considérese un ejemplo, aprovechando lo visto en el tema de representación de datos: se codificarán numéricamente los elementos de los conjuntos Q, A y D y se codificarán también la entrada y la salida escritas en la cinta. Se hará una máquina que incremente en uno un número dado como entrada, este número será dado como una secuencia (posiblemente vacía) de unos consecutivos en la cinta de entrada (comenzando en la celda inicial). Así, para dar como entrada el número 5, se debe proporcionar una secuencia de cinco 1 consecutivos en la cinta. Se asumirá que las celdas desocupadas de la cinta contienen un cero. La máquina comienza en la celda inicial al comienzo de la secuencia de entrada. En ese estado se permanecerá recorriendo la cinta (es decir, cada vez que se encuentre un 0 se reemplaza por el mismo 0) hasta que se encuentre el primer 1 de la secuencia de entrada, se cambia entonces al estado 2 recorriendo la entrada completa (ahora se hace lo complementario, sobrescribiendo los 1 que se encuentran) hasta el primer 0 a la derecha de ésta; en ese momento se le reemplaza por un 1 y se pasa al estado que indica que se ha terminado la ejecución (el estado qF ). La cabeza termina en la primera celda a la derecha de la salida. En la siguiente tabla se muestra la especificación completa de esta máquina de Turing.
Limitaciones de la máquina de Turing
Una vez que se tiene un modelo de una computadora, cabe preguntarse cuál es su poder, qué cosas puede computar y cuáles no. Turing pudo así probar que existen problemas no computables, que no se pueden resolver mediante una máquina de Turing. Una manera relativamente simple de probar esto es notando lo siguiente:
Hay más problemas que máquinas de Turing
¿Cuántas posibles máquinas de Turing existen? A fin de cuentas, una máquina de Turing cualquiera es una lista de quintetas (a, x, e, y, d), donde cada una de las variables está tomada de un conjunto finito. Si de momento se considera que las quintetas no forman parte de una lista y se eliminan las comas que separan los elementos de cada una, queda una secuencia de números, aquellos con los que se codifican los elementos. Todo esto no es, de hecho, más que un número, posiblemente muy grande, pero un número a fin de cuentas. En el ejemplo, leyendo los números de la tabla de arriba abajo y de izquierda a derecha se tiene: 110121123112113302312. Podría usarse esto como el nombre de la máquina y de hecho identificar a cualquier máquina por el número entero que se obtiene de leer su tabla completa. Puede pensarse ahora que cualquier número entero no negativo puede verse, en efecto, como la tabla de una máquina de Turing, a lo mejor una muy inútil, por ejemplo una que, sin importar la entrada, siempre escriba un 1 y termine. Habrá otra que recorra tres lugares hacia la derecha y termine sin hacer nada, y también varias iguales que sólo avancen cinco lugares a la derecha, tres a la izquierda y escriban un 8, en tanto que otra calcule el trigésimo séptimo dígito de π. En fin, habrá muchas máquinas de Turing, válidas sin duda, aunque algunas sin sentido. Pero lo importante aquí es que puede concluirse que hay tantas máquinas de Turing como números naturales, es decir, el número de máquinas de Turing es infinito y numerable (al igual que los números naturales, pueden recorrerse de uno en uno). Mientras que no es difícil mostrar que el número de problemas es infinito no numerable —esto es, hay tantos como números reales existen—, un número estrictamente mayor que el de números naturales.
Las máquinas de Turing resultan de poca utilidad cuando se trata de determinar la complejidad de un algoritmo, o para planear la construcción de una computadora. El modelo es demasiado simple, pero de muy alto nivel de abstracción. Por ejemplo, no representa explícitamente el programa que se está ejecutando, su lista de instrucciones.
Esto da lugar a otra abstracción, como la denominada máquina de acceso aleatorio (RAM, por sus siglas en inglés), del estilo de la arquitectura de von Neumann, que son más cercanos a la forma en la que está construida una computadora moderna pero con exactamente el mismo poder de cómputo que una máquina de Turing. En el capítulo de computadoras se verá esto con más detalle. Ésta es, esencialmente, una abstracción de la máquina real en la que el algoritmo, luego de ser traducido a un programa, será ejecutado. En el modelo RAM se supone que las instrucciones o pasos que constituyen el algoritmo son ejecutados secuencialmente, uno tras otro; ningún paso se ejecuta al mismo tiempo o con un traslape temporal con otro. Los recursos consumidos durante la ejecución son contabilizados, eliminando detalles de manera uniforme, así que, en general, cada paso del algoritmo tarda lo mismo cada vez que se ejecuta.
Todos los algoritmos que se han tratado en este texto han sido inicialmente mostrados en una especie de lenguaje adecuado para que el procedimiento pueda comprenderse sin malos entendidos, a los que se les suele llamar seudocódigos. No han sido escritos en un lenguaje de programación específico. Éstos se pueden representar mediante una máquina de estados, como el modelo RAM. Sin entrar en detalles, este modelo define una memoria donde están almacenadas una tras otra las instrucciones del programa, y un lugar especial de la memoria con un número que indica cuál es la siguiente instrucción a ejecutar.