Una de las primeras ramas de la ciencia que cultivó la humanidad es la geometría. Euclides, en el siglo II antes de nuestra era, formuló los principios fundamentales de lo que hoy se denomina geometría sintética. En este tipo de geometría, las únicas operaciones válidas son aquellas que pueden llevarse a cabo usando solamente una regla (sin graduar, por lo que no se puede "medir" con ella y solamente se pueden trazar líneas rectas) y un compás, y existen algoritmos con estas operaciones para obtener innumerables construcciones geométricas. Aunque no todas.
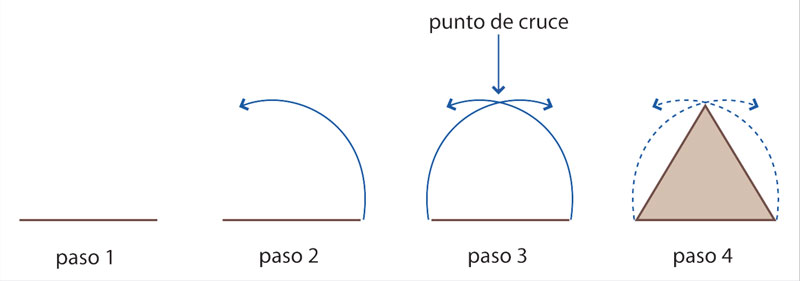
Para construir un triángulo equilátero, por ejemplo, se tiene el siguiente algoritmo:
1] Se traza un segmento de recta de longitud arbitraria.
2] Se apoya el compás en un extremo del segmento y se abre hasta el otro. Se traza el arco de circunferencia usando ese punto de apoyo y esa apertura.
3] Se apoya el compás en el otro extremo del segmento y se traza otro arco de circunferencia sin cambiar la apertura.
4] Se elige como vértice del triángulo uno de los puntos en donde se cruzan los arcos y se trazan los segmentos que van desde él hasta los extremos del segmento.
Curiosidades
La teoría de Galois ha logrado responder a la pregunta de qué problemas se pueden resolver utilizando sólo regla y compás. Pero no se sabe mucho acerca de la complejidad de éstos. Es decir, acerca de cuántos pasos son necesarios para resolver un problema dado.
También hay algoritmos que permiten trazar un pentágono, un hexágono o dividir un ángulo en dos partes iguales, por ejemplo. Sin embargo, los geómetras griegos buscaron sin éxito un algoritmo para llevar a cabo las siguientes construcciones:
• La trisección del ángulo: dividir un ángulo en tres partes iguales.
• La duplicación del cubo: dado un cubo, construir otro cuyo volumen sea el doble del primero.
• La cuadratura del círculo: dado un círculo, construir un cuadrado de la misma área.
Todas éstas, por supuesto, han de hacerse con sólo regla y compás. Es aquí donde reside el problema. Pasaron siglos antes de que los matemáticos lograran demostrar, en el siglo XIX, que no existe algoritmo que resuelva estos problemas usando sólo regla y compás. Es decir, resultan no computables en la máquina abstracta de la geometría sintética, cuyo lenguaje está hecho sólo de operaciones con esos dos instrumentos.
Hoy en día, en cambio, se suele estudiar la geometría analítica creada por Descartes en el siglo XVII; en ella se introduce el concepto de sistema coordenado y se formulan expresiones algebraicas que corresponden con las construcciones geométricas. Usando las herramientas, o el lenguaje de la geometría analítica, los tres problemas mencionados sí tienen solución y, de hecho, no es complicada.