Preguntarse si las máquinas pueden pensar es como
preguntarse si los submarinos saben nadar.
EDSGER W. DIJKSTRA.
Mucho de lo referente a computación es acerca de máquinas de estado. Las máquinas de estado son para los computólogos lo que las ecuaciones son para los físicos. Casi cualquier fenómeno que tenga que ver con computación puede ser descrito mediante una máquina de estado. De hecho, como dice Leslie Lamport, dado que las máquinas de estado pueden ser descritas y manipuladas mediante matemáticas ordinarias y cotidianas, es decir, conjuntos, funciones y lógica sencilla, éstas proveen un marco de trabajo uniforme para estudiar el cómputo de manera formal, con matemáticas sencillas.
—Hola, Úrsula, mira lo que compré en el mercado de antigüedades.
—¿Para qué sirve? Es sólo una caja con una luz verde, un botón de reset y un micrófono
—le contesta a Arcadio.
—Pues ni idea. Sólo sé que cuando le dices palabras, a veces se prende la luz verde y a veces no.
—Pues ábrela y mira qué tiene adentro.
—Traté pero no pude. No tiene tornillos, está muy bien sellada.
—A ver —dice Úrsula—, le voy a decir algo: hola.
La luz verde no se prende. Después de varios intentos, como "perro", "loca" y "Arcadio", para los cuales la luz no se prendió, Úrsula dice:
—Creo que tu caja no sirve… a ver, haz otro intento: "Francia". ¡Se prendió la luz!
—París. Uy, no se prendió. España. ¡Se prendió otra vez!
—México. No se prendió. Canadá. Tampoco. China. Tampoco.
—Italia. ¡Sí, otra vez se prendió!
Después de jugar un buen rato con la caja, deciden que sirve para indicar los países de la Unión Europea, ya que cuando le dicen a la caja un país de otro continente la luz no se prende.
Los computólogos le llaman a esto "caja negra", ya que su apariencia no da ninguna pista acerca de su función, de su comportamiento, ni de cómo está construida, o de qué materiales. Pero ya sea que su mecanismo esté hecho de engranes de metal, de circuitos electrónicos o de un ratón muy listo, el hecho es que se debe suponer que entre palabra y palabra, cuando no hay actividad, sus partes internas se estabilizan configurando un estado, sin saber qué signifique exactamente esto (podría ser niveles de voltaje o posiciones de los engranes, por ejemplo). Lo cierto es que se puede suponer que el número de estados posibles de la caja es finito; un cierto número, quizá grande, pero finito, ya que la caja en sí es finita. Al inicio, la caja se encuentra en uno de esos estados, considerado el inicial. El botón de reset sirve precisamente para regresar a la máquina a este estado. Ahora bien, cuando le dicen una palabra a la caja, lo único que se puede saber es que produce una salida (prende o no la luz) y cambia a otro estado (que podría ser el mismo en el que estaba). Así que, aparentemente, sin necesidad de saber nada acerca de la caja negra, se puede describir su comportamiento mediante un autómata finito, es decir, una gráfica cuyos vértices son los estados, y arcos dirigidos de un vértice a otro etiquetados con las entradas y salidas posibles.
Como ya se ha discutido en el tema 4, se puede suponer que tanto las entradas como las salidas son bits que podrían estar codificando palabras, sonidos o cualquier otra cosa. Ignorando de momento qué representan; a final de cuentas, es sólo una caja negra, y no hay manera de saber su "intención". Solamente se obtienen secuencias de salidas al darle entradas. En la figura 1 aparece un autómata de siete estados; sobre cada arco está indicada la entrada que ocasiona que transite al estado al final del arco.
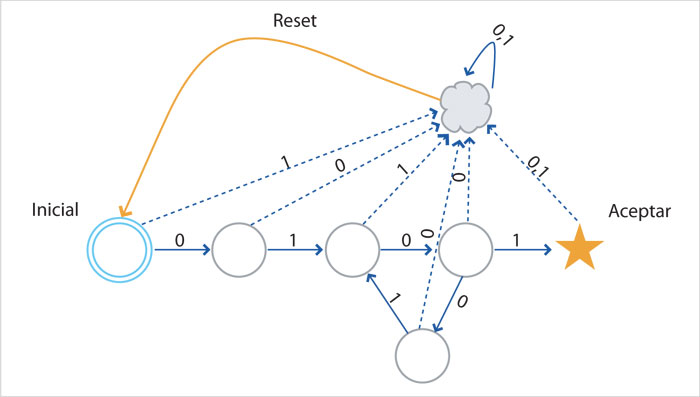
En este autómata hay tres entradas posibles: 0, 1 y reset, y de cualquier estado, al darle reset, se llega al estado inicial (aunque no se pintaron todas las líneas de reset para no abarrotar la figura). Se puede pensar en que al llegar al estado aceptar, se prende la luz verde.
¿Qué hace este autómata? Acepta la cadena 0101, la 0100101 y, en general, la cadena que empieza con 010, seguida de 010 tantas veces como se quiera (quizá cero veces), y terminar con 1. Es decir, acepta todas las cadenas de la forma 010(010)*1. Que haya otros autómatas que aceptan el mismo conjunto de cadenas es una indicación de lo que ya se suponía. Hay muchas maneras de implementar la misma caja negra, así que para un observador externo es imposible distinguir una de otra.
Cajas negras y limitaciones de la ciencia
Ahora bien, ¿hay manera de que Arcadio y Úrsula descubran cuál es el autómata que representa el comportamiento de la caja negra? Esto es, como observadores externos, pueden probar más y más cadenas de entradas y observar las salidas producidas, pero nunca pueden probar todas las cadenas de entrada, porque hay un número infinito de éstas. Saben que la caja tiene un número finito de estados, pero no saben cuántos tiene. Si descubrieran un letrerito pequeño debajo de la caja que dijera "Caja negra modelo X42901 de 5 estados" podrían saber con toda exactitud cuál es el conjunto de cadenas que acepta (es demasiado difícil explicar cómo hacer esto en un texto introductorio a la computación). El hecho es que sin esta información es imposible determinarlo: por más y más entradas que le den a la caja negra, siempre puede haber una para la cual se comporte de manera inesperada. Recuérdese el fenómeno del Cisne Negro descrito en el tema 2. No porque sólo se conozcan cisnes blancos quiere decir que todos los cisnes son blancos. Esto nos habla de una limitante inherente a la ciencia en general. Que una ley física se cumpla no quiere decir que sea "verdadera", sólo que se observa su cumplimiento en todos los experimentos realizados.
Durante cientos de años se pensó que las leyes de Newton eran verdaderas hasta que llegó Einstein y demostró que no, al menos no del todo. Que se haya observado durante siglos que se cumplían significa que no estaban tan mal. En efecto, casi siempre se cumplen. En algunas situaciones de extrema velocidad no. Así que en realidad las teorías de Einstein depuraron las leyes de Newton. Así funciona la ciencia, como una sucesión de aproximaciones que describen cada vez mejor los fenómenos de la naturaleza. Al igual que las cajas negras, mientras más entradas se prueben, mejor se les podrá describir.
En cualquier procesador de palabras o en cualquier programa editor se tiene, por ejemplo, la función de búsqueda. En casi todos ellos existe además la opción de buscar todas las cadenas de texto que satisfagan ciertas características, por ejemplo, todas la cadenas que terminan en "ando" o las que empiezan con una "a", luego tienen alguna otra letra y después otra "a". Generalmente, para denotar estos conjuntos de cadenas se utiliza lo que se denominan expresiones regulares: el primer ejemplo sería *ando, el segundo a?a*. Para realizar este tipo de búsquedas se usan autómatas finitos.
Cada expresión regular define por sí misma un conjunto de cadenas de símbolos, llamadas palabras. En el primer ejemplo están consideradas las cadenas "silbando" y "caminando", pero no "ayer" o "silbar"; en el segundo ejemplo están "ana", "alas", "anazasi" y "amante", pero no "amor" o "banana".
Un resultado importante, y quizás sorprendente, de la teoría de la computación es que los autómatas finitos definen conjuntos de palabras que provienen de expresiones regulares y nada más esto. Son muy útiles, como se puede comprobar cuando se usa un procesador de texto, pero ciertamente su utilidad es limitada. Por ejemplo, no existe ningún autómata finito que reconozca los palíndromos marcados; es decir, todas las cadenas de la forma zmz', donde z' es la misma cadena que z, pero escrita al revés, y m es una letra especial que marca el centro del palíndromo. Hay muchas cosas, inclusive sencillas, que no son computables por medio de un autómata finito.
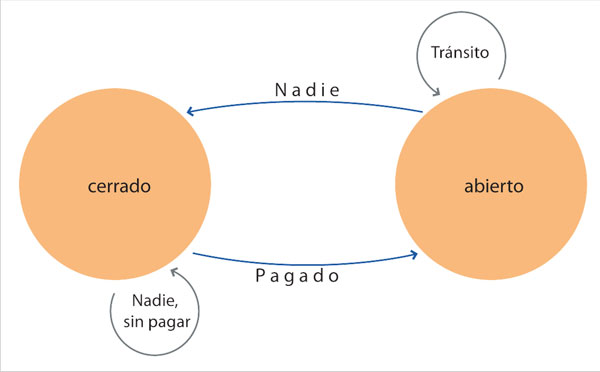
Resultan insospechadamente usuales las aplicaciones de los autómatas finitos: en estacionamientos y edificios públicos es cada vez más frecuente encontrar puertas automáticas, cuyo funcionamiento está regulado por un autómata finito. El siguiente diagrama ilustra la operación de la pluma de un estacionamiento automático.
La pluma puede estar en uno de dos estados posibles: abierto o cerrado. Si no se está procesando ningún boleto de estacionamiento —es decir, no hay nadie en la pluma—, entonces permanece en ese estado; lo mismo ocurre si el boleto que se introdujo no ha sido pagado. Si el boleto ha sido pagado entonces se pasa al estado abierto, donde se permanece mientras no haya pasado el cliente con su automóvil, es decir, mientras esté en tránsito. Una vez que el cliente ha pasado, se regresa al estado cerrado.
Otro caso popular es el de las máquinas expendedoras de golosinas. Una vez que se ha depositado el dinero entra en operación una máquina de estados finitos. Cada estado está asociado a una de las posibles golosinas disponibles, se gira el resorte que empuja la seleccionada hasta que cae y la que sigue ocupa su lugar. Luego se pasa al estado (mejor dicho, conjunto de estados) en que se entrega el cambio.
Máquinas de estados y lenguajes
Como ya se mencionó en el tema de Algoritmos, una computadora entiende un lenguaje en el que se escriben los algoritmos que es capaz de ejecutar. Ese lenguaje es una manera de describir un modelo de la máquina que representa esa abstracción, se puede decir que lo esencial de la máquina es que puede hacer sumas y multiplicaciones, por ejemplo. Los algoritmos que debe ser capaz de ejecutar están dados en términos de esas operaciones y no otras. De hecho, el lenguaje de la computadora abstracta define lo que ésta puede hacer. Dado el lenguaje de la máquina habrá cosas que no puedan expresarse como algoritmo, porque no podrían escribirse en términos del lenguaje propio de la máquina. Máquinas de estados y lenguajes son dos caras de una misma moneda. A continuación se presentará el ejemplo de un modelo de cómputo descrito a partir de un lenguaje.